Prozentrechnen = Dreisatz
Auf dieser Seite:
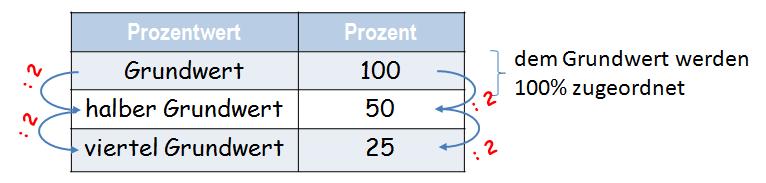
Auf der letzten Seite wurde der Grundwert als die Menge/Anzahl definiert, welcher 100% zugeordnet werden. Ein Prozentsatz von 50% ist gleichbedeutend mit der Hälfte des Grundwertes und ein Prozentsatz von 25% ist gleichbedeutend mit einem Viertel des Grundwertes:
Man sieht also: Halbiert sich bei gleichbleibendem Grundwert der Prozentsatz, dann halbiert sich auch der Prozentwert! Verdoppelt (verdreifacht, vierfacht, …) sich der Prozentsatz, dann verdoppelt (verdreifacht, vierfacht, …) sich auch der Prozentwert.
Es besteht also dieser für die Prozentrechnung sehr wichtige Zusammenhang zwischen Prozentsatz und Prozentwert:
Zusammenhang Prozentsatz ↔ Prozentwert
Bei gleichbleibendem Grundwert stehen der Prozentsatz und der Prozentwert in einer direkt proportionalen Zuordnung.
Für die Prozentrechnung können somit die Methoden der Dreisatz-Rechnung angewendet werden!
Dreisatztabelle erstellen
Um eine Aufgabe der Prozentrechnung zu lösen, kann man also stets eine „Dreisatz-Tabelle“ zeichnen und diese Informationen eintragen:
In jeder Aufgabe ist einer der drei Werte Grundwert, Prozentsatz oder Prozentwert nicht gegeben und soll stattdessen berechnet werden. Hierfür ist der Zwischenschritt mit dem Schluss auf die Einheit in der noch freien Zeile der Tabelle notwendig.
Für jeden dieser drei Aufgabentypen erfolgt jeweils eine ausführliche „Schritt-für-Schritt“-Erklärung auf den nächsten Seiten.
Weiter geht’s mit: Fragen zu Schritt 1: Grundlagen der Prozentrechnung