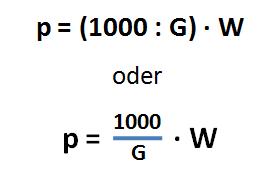|
Aufgabe: Promillesatz berechnen
Der Promillesatz p‰ lässt sich direkt berechnen, indem man den Promillewert W durch den Grundwert G dividiert und anschließend mit 1000 multipliziert. Als Formel lässt sich das so schreiben:
Falls Du eine anschauliche Erklärung mit einem ausführlichen Beispiel haben möchtest, dann lies bitte im Kapitel Rechnen mit Promille nach
A) Lösung mit Hilfe der Formel
Schritt 1: Was ist gegeben?
| gegeben: | W | = 16 | (Promillewert) |
| G | = 1600 | (Grundwert) |
Schritt 2: Was ist gesucht?
| gesucht: | p‰ | = ? | (Promillesatz) |
Schritt 3: Welche Formel ist anzuwenden?
Schritt 4: Werte in Formel einsetzen und berechnen
Variante 1: Taschenrechner
p = (16 : 1600) * 1000 = 10
p‰ = 10‰
Variante 2: Bruchrechnung
| p = | 16 | * 1000 = | 16 * 1000 |
| | | ||
| 1600 | 1600 |
| = | (16 : 16) * 1000 | = | 1 * 1000 |
| | | ||
| 1600 : 16 | 100 |
| = | 1 * (1000 : 100) | = | 1 * 10 |
| | | ||
| 100 : 100 | 1 |
| = | 10 | = 10 |
| | ||
| 1 |
p‰ = 10‰
B) Lösung mit Hilfe des Dreisatz
Schritt 1: Was ist gegeben?
| gegeben: | W | = 16 | (Promillewert) |
| G | = 1600 | (Grundwert) |
Schritt 2: Was ist gesucht?
| gesucht: | p‰ | = ? | (Promillesatz) |
Schritt 3: Werte in Dreisatz-Tabelle eintragen
1) Dem Grundwert G = 1600 entsprechen 1000‰.
2) Gesucht ist der Promillesatz p = x Promille, welchem der Promillewert W = 16 entspricht.
| Promillewert | Promille | Bemerkung |
| 1600 | 1000 | G = 1600 entsprechen 1000‰ |
| 16 | x | Wieviel Promille entspricht W = 16? |
Schritt 4: Schluss auf die Einheit
| Promillewert | Promille | Bemerkung |
| 1600 | 1000 | Teile durch G = 1600 |
| 1 | 0,625 | 1 entspricht 0.63‰ |
| 16 | x |
Schritt 5: Schluss auf das gesuchte Vielfache
| Promillewert | Promille | Bemerkung |
| 1600 | 1000 | |
| 1 | 0,625 | Multipliziere mit W = 16 |
| 16 | x = 10 |
Schritt 6: Ergebnis aus Tabelle ablesen
16 sind 10 ‰ von 1600.